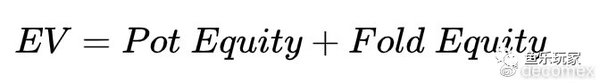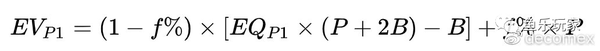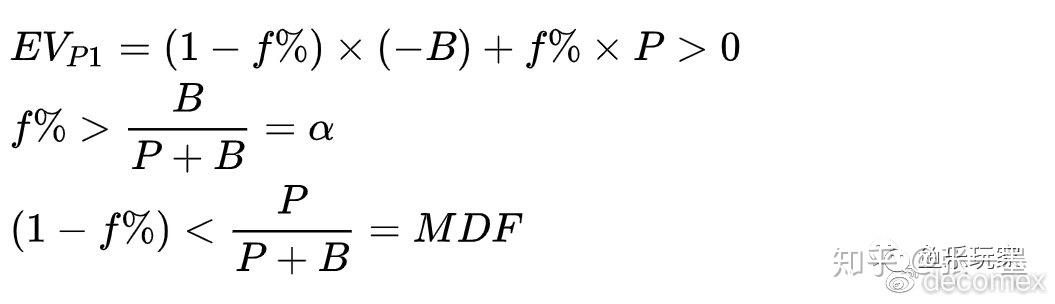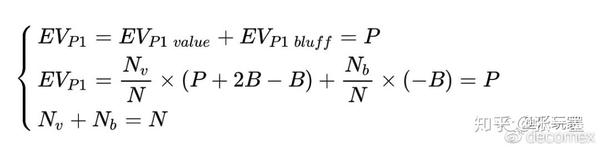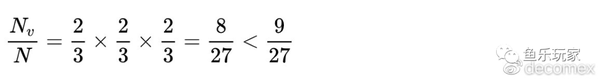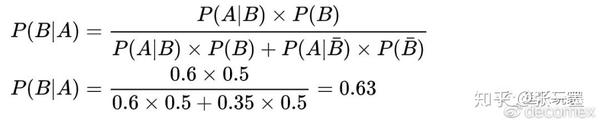这些话本来是要放在最后说的，可是我怕你们看不到那里！下面的内容太过于硬核，看到那些数学公式，心里就已经一万头草泥马奔腾而过了，但是不妨碍你去了解GTO背后的理论依据，凡事就算我们搞不懂具体过程，可是背后的原理我们应该了解，如果你是一个理性思维的人，你应该懂，当你了解背后的原理，就不会那么轻易的被人当成韭菜割掉，这就是韭菜该有的自我修养。

就好比那些花里胡哨的各种减肥代理，什么营养代餐啦等等，其实减肥的原理只有人体摄入热量<消耗热量，你就会瘦，其他的原理都是扯淡，想减肥要么从摄入上下手，要么从消耗上下手，其他的都是耍流氓！动辄几千上万一个疗程的各种名目的减肥真的都是智商税！敲黑板，智商税啊！！！
玩德州扑克最重要的是什么？当然是赢啊！赢才有乐趣，谁他么天天输还能体会的到巨大无比的乐趣的？如果有，请你赶紧联系我，我会让你的乐趣double,triple,quadruple(四倍的英文知识点啊记一下)！
那么问题又来了？这些大神已经牛逼到这种程度了他们研究的东西我看都不看不懂，怎么赢他？很简单，不跟他们打，你就赢了！大多数情况下我们接触到的牌局级别和我们能够上桌游戏的级别游戏水平是没那么高的，你所储备的扑克技术足够应付你现在所打的牌局就可以了，至于更高深的技术我们只需要在各种豪客赛的视频里看大神们操作就好了，挑选好你的对手才是胜率的最好保障。德州扑克就是这么一种“欺软怕硬”“看人下菜碟”的游戏！


为了方便理解下面的内容，先科普几个基本概念：
GTO（Game Theory Optimal）是指在德州扑克上理论的最佳策略
EV（Expected Value）期望=盈利*预估胜率+损失*预估负率
接下来就是硬核的内容,转自微博用户名：decomex


1. EV公式与Action
1.1 基本EV公式








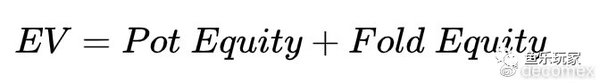
无论采用何种策略，基本EV公式都是一样，由底池权益和弃牌权益组成。
主动方（Aggressive: Player1）的EV扩写成：




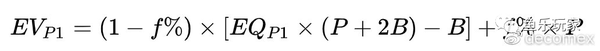
被动方（Passive: Player2）的EV扩写成：




· EQ--P1和P2所占的底池权益（胜率）百分比；
· f%--P2（防守方）的弃牌频率（Fold Frequency）；
· P--当前底池的大小；
· B--P1（进攻方）的下注大小。
对HU来说：








· 表明：在P2（被动方）确认跟注之前，无论P1（主动方）采用什么尺度下注博彩问答，他的总EV不会超过底池大小。


1.2 从EV公式中分析行动的意义


BET：主动方下注博彩问答，理由一：确认己方当前的底池（P）权益，并尝试将底池扩大到（P+2B），以增加己方的所占底池权益的绝对值（EV）；理由二：确认己方当前的底池（P）权益，并尝试拒绝对方当前的底池权益，以获得对方的弃牌权益。
CALL：被动方跟注，确认对方扩大底池（P+2B）后，己方的底池权益。
FOLD：被动方弃牌，放弃己方的底池（P）权益，结束当前牌局。
CHECK：OOP过牌，确认己方当前的底池（P）权益，并放弃获得对方的弃牌权益。IP过牌，确认己方当前的底池（P）权益，并进入下个回合或秀牌。
RAISE：被动方加注，确认对方扩大底池（P+2B）后，己方的底池权益。然后转换主动与被动方， 并尝试将底池扩大到[P+2B+2x(R-B)]，理由同下注。




2. EV公式的推导








2.1 Odds（底池赔率/赔率）


Pot Odds/Odds，是在EV公式去掉f%的影响，只考虑EQ。
前提：Odds应用于被动方P2的弃牌率f%=0%时（即跟注）。


当进攻方P1在底池P中下注B时，对防守方P2来说，Fold的EV永远是零。如果防守方决定跟注防守，必然需要EV_{P2}>0。










同时，上述的百分比形式底池赔率经常改写成1赔多少的赔率：












· Odds代表着1赔多少，这是各种博弈/博彩游戏中常用的一个参数。
· Odds可以用于翻前及翻后各条街。
· 对P2来说，EQ_{P2}是Hand vs Range。


2.2 MDF（最小防守频率）


MDF(Minimum Defense Frequency)，是在EV公式去掉EQ的影响，只考虑f%。


前提：MDF应用于被动方P2防守，而P1是两级化范围时，常见的是河牌。


当进攻方P1在底池P中下注B来进行BLUFF时，即EQ_{P1}=0%时，要使EV_{P1}>0。










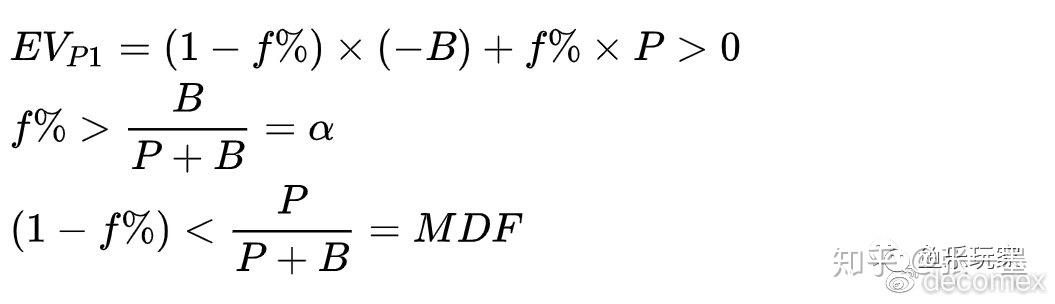
· 即P2的跟注必须小于MDF，P1才能用EQ_{P1}=0%的牌获利。
· 对于防守方P2来说，大于MDF的跟注频率才能阻止P1用ATC（any two cards）诈唬获利。
· 在河牌中，如果判断出对手是两极化范围（Polarized Range），那么可用MDF频率抓诈。
2.3 价值诈唬比


前提：价值诈唬比应用于主动方P1下注。


当主动方P1在底池P中下注B时，要使被动方P2跟注与弃牌无差别，即EV_{P2}=0，EV_{P1}=P。
假设P1范围内有N手牌，其中N_{v}手EQ=100%，N_{b}手EQ=0%。








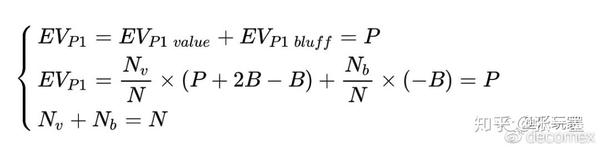
因此，当P1是两极化范围时，他的下注时价值诈唬比为：










· P1的价值比诈唬，在数值上等于P2的Odds（赔率）。
· P1的诈唬比价值，在数值上等于P2的α（弃牌频率）。


2.4 MDF的局限


· 应用MDF（P2）出现的问题，在于假设P1的Bluff手牌的EQ都是零，Value手牌的EQ都是100%。


· 也就是说，主动方P1必须在每条街上都是完美两极化范围（Polarized Range），而被动方P2始终是紧缩范围（Condenced Range）。


· 事实上，在非河牌圈，这种情况非常罕见。


· 但是在翻前/翻后前两街，MDF（P2）与价值诈唬比（P1）仍提供了我们一种思路。我们应该用EQ高（强成牌）、EQr>1（强听牌）的手牌来组成的两极化范围进攻，EQr接近1（弱成牌）组成的紧缩范围防守，而EQ低和EQr<1（垃圾牌）弃牌。










3. 逆向归纳法


3.1 方法与实例


逆向归纳法，Backward Induction，常用于求解动态博弈的纳什均衡（子博弈精炼纳什均衡SPE）。其基本思路是从动态博弈中的最后一个阶段开始，局中人都遵循EV最大化选择行动，然后逐步倒推至前一个阶段，一直到博弈开始局中人的行动选择。


Subgame Perfect Nash Equilibrium（SPE），Perfect的意思是要求在每一个子博弈（Subgame）节点都达到Nash Equilibrium，从而消除静态NE中不可置信的威胁的问题。
举一个NLH Toy Game的例子来说明完美极化范围（PR）和逆向归纳法（BI）：


· OOP RANGE：AA、7♥2♥、7♠2♠
· IP RANGE: KK
· Borad：A♠A♣K♣
· Staring Pot=100，Effective Stacks=1300
· OOP在Flop下注100，已知OOP的策略是三条街各下注100%Pot Size
· 求解IP的应对策略？
在这个Toy Game情景设置中，我们可以看到OOP在三条街都形成了完美的Polarized Range，并具有稳定的胜率。现在以逆向归纳法来求解IP在Flop的应对策略。
从河牌开始推算，OOP下注100%底池，下注范围具有1个价值，0.5个诈唬，价值诈唬比是2:1。他可以选择1个AA，0.5个72，而如果IP能坚持到河牌，按MDF要求，他应该防守50%的KK。
倒推到转牌，OOP下注100%底池，他的下注范围应该是1.5个价值，0.75个诈唬，他选择推进到河牌的下注范围是{1个AA，0.5个72}，推进到河牌的过牌范围是0.75个72。
倒推到翻牌，OOP下注100%底池，他的下注范围应该是2.25个价值，1.125个诈唬，他选择推进到转牌的下注范围是{1个AA，1.25个72}，推进到转牌的过牌范围是1.125个72。而实际上，在剔除价值牌后，推进到转牌的过牌范围只剩下0.75<1.125，以通俗的语言讲，在Flop上OOP的诈唬不足。








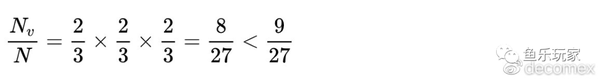
解答：IP得知这个策略后，KK的唯一选择是弃牌。


3.2 几个疑问


问题一，IP在翻牌可以用Odds吗？
A: 在翻牌OOP下注100%P，给到IP的Pot Odds是33%，而对应OOP的范围，KK对1个AA，2个72，EQ_{P2}=66%，表面看来赔率合适。为什么不能Call呢？这就是Odds的问题，因为它是静态的，无法考虑对手后续的策略。如果我们的SPR极低或牌局就在此刻结束，才能用Odds跟注。
问题二，OOP为什么一直用价值咋呼比？
A: 价值咋呼比是用下注额来分配极化范围的要求，也是GTO的关键点之一。
问题三，我们在河牌能用到MDF吗？
A: 由于KK的最优策略是在Flop就弃牌，所以按MDF计算河牌抓诈已经毫无意义。如果IP跟注到河牌，我们称之为Off-tree，也就是该行动已经在Flop偏离了IP的最佳策略。反映在Solver上，就是这个组合在河牌已经没有任何行动频率。
问题四，如果OOP不懂均衡策略，不按这个策略线行动，IP应该怎么做？
A: 这就是我们需要建立策略树的原因。多条可能策略线形成策略树，每条策略树的结果聚合后，构成一个IP在Flop行动的频率。
4. Solver存在的问题与贝叶斯定理


在Solver中，一共有49张未知转牌、48张未知河牌，一共是2352个组合。我们建立了若干条策略线，每条策略线对应的2352个组合，分别进行逆向归纳法计算。最后的结果以聚合的形式，在Flop进行汇总，从而得到GTO解。
Solver本质上是一个SPE（子博弈精炼纳什均衡）计算器。而NLH，是一个不完全信息动态博弈游戏，要用PBE(Perfect Bayes Equilibium精炼贝叶斯纳什均衡)来解决。当存在不完全信息时，逆向归纳法并不能用来解决PBE问题。
因此，我们用solver，事实上是把对手的范围观察后转化为完全信息，再用抽象过的策略树来尽量模拟整个策略空间。然后，把PBE降阶为SPE来计算。
这就产生Solver的两大问题：第一，如何利用贝叶斯推断对手的信念（范围）？；第二，Solver解对树外的未知策略的鲁棒性如何？
4.1 贝叶斯定理浅探


应用贝叶斯定理需要一个先验概率，基于新的信息，修正后验概率。
一个简单的例子：一个未知牌手第一手就在BTN位RFI抢盲，而你在BB位置。你判断他有先验概率50%可能是35%范围的紧手，有先验概率50%可能是60%宽范围的松手（35%、60%来源于我们对当前玩家池的总体大数据）。他是宽范围松手的后验概率变化为多少？
令事件A为对手在BTN位置抢盲；
令事件B为对手是宽范围的松型牌手。








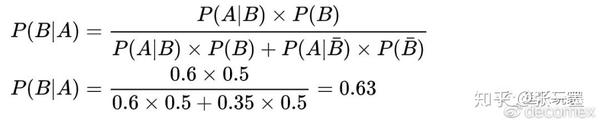
紧接着第二手他又在BTN位RFI抢盲。你已修正他有先验概率37%可能是35%范围的紧手，有先验概率63%可能是60%宽范围的松手。他是宽范围松手的后验概率又变化为多少？










紧接着第三手他又在BTN位RFI抢盲。你已修正他有先验概率17%可能是35%范围的紧手，有先验概率83%可能是60%宽范围的松手。他是宽范围松手的后验概率又变化为多少？










因为他连续三手RFI抢盲，我们判断他96%的可能是一名60%宽范围松手。我们在Solver输入他的范围时，在NE的基准范围上，可暂时按60%左右的范围放宽。
也许你从直觉已经判断出相同的结果，但贝叶斯定理给了我们观察分析对手的数学依据。


4.2 树外策略问题


我们说的树外策略，不是指45%Pot Size和50%Pot Size，这些尺度都可以人脑中进行抽象归并。特定的树外策略例如人机大战，为了寻找Libratus的漏洞，人类选择了各种匪夷所思的尺度，如5%，300%等。根据资料，在PIO中，10%以下的下注是被忽略的。
但这并不代表Solver不能付诸于实践。事实上，由于现实游戏中人类的筹码深度和行为习惯，常见的下注尺度从25%-150%之间，Solver中建立的策略树基本可以反映现实情况，我们没有必要将不可能发生的策略加入策略树以增加解的复杂度。
使用Solver尽量细化优化策略树（根据计算机能力），来得到相对准确的有鲁棒性的解。这是一个要研究的方向。
5. 总结
对于GTO策略和应用软件Solver，我们既不应该无限神化，也不应该随意贬低。GTO策略是根据扑克基本原理导出的一种均衡策略，而Solver是一种有用的学习工具和计算器。
没有Solver，你也应该要了解扑克背后的博弈论原理、基本EV公式、逆向归纳法和贝叶斯定理。