2017年1月30日，在宾夕法尼亚州匹兹堡的Rivers赌场，卡耐基梅隆大学（CMU）开发的人工智能系统Libratus战胜4位德州扑克顶级选手，获得最终胜利。



四名扑克选手：Daniel McAulay （左一），Jimmy Chou（左二），Jason Les（右二）、Dong Kim（右一）。人工智能Libratus的项目主任（左三），工程师（右三）
自从任从围棋之后，人工智能有新突破。围棋总共可能有10^171种可能性，而德州扑克也有高达10^160种可能性，远超当今电脑运算能力。
另外，德州扑克不同于围棋，象棋之处在于，由于对方的“底牌信息”是隐藏信息，对于计算机来说，就是在处理一种“非完整信息博弈”，而围棋对弈双方的信息是完整的、对称的，并没有隐藏的信息。Libratus此次战胜顶级人类德州扑克选手，具有非常重要的意义。
世界上众多领域的问题，如谈判，军事对抗，经济，互联网安全，都包含大量未知信息，解决德州扑克的人工智能技术会在众多领域得到应用。
此次由4名世界顶级扑克职业玩家：Jason Les、Dong Kim、Daniel McAulay 和Jimmy Chou对战人工智能程序Libratus，赛程为20天，一共进行了12万手牌的比赛。最后人工智能以1766250分的优势战胜4位人类选手。

比赛模式：
比赛模式为1对1（head up）德州扑克，在20天内，4位人类玩家总共打12万手，每位玩家各自与人工智能进行3万手牌1对1德州扑克。平均每天打1500手牌，进行10小时比赛，每小时打150手1对1德州扑克。
大盲注，小盲注分别为$100，$50，每手牌的筹码为200个大盲注。当一手牌结束后，双方筹码都重新设定为$20000分。这是为了减少上一手牌对下一手牌的影响，减低运气成分对比赛结果的影响。
比赛模式类似以下网络扑克应用 Play Texas Holdem Against Strong Poker Ai Bots ， 这款扑克AI名称叫HibiscusB，能战胜中级水平的扑克玩家，但没有Libratus强大。
应用界面如下，扑克迷可以到这个网站与AI对局，体验一下。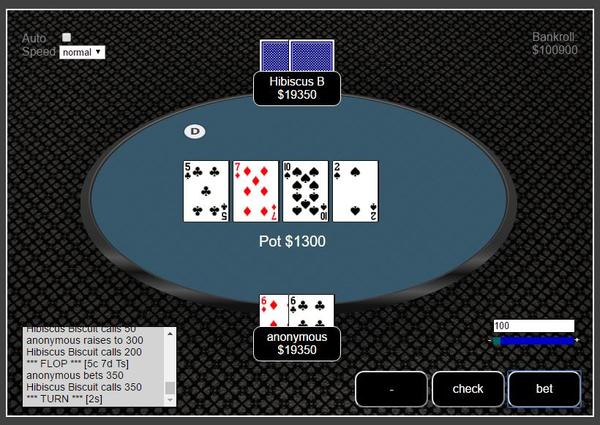




比赛结果分析：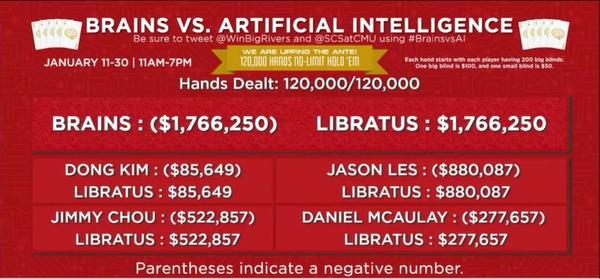




4位扑克选手总共输给人工智能Libratus 1766250分，即17662.5个盲注（大盲注100分）。其中Dong Kim 的成绩最好，但也输掉了85649分，即856个盲注。成绩最差的Jason Les 输掉了8800个盲注。
人类顶级的4位扑克玩家在12万手牌共输掉17662.5个盲注，平均每100手牌输14.7个盲注。以每小时打150手牌的速度，平均每小时要输掉22个盲注。
这是什么概念，按当前中国大多数地下德州扑克的游戏，通常玩5/10元大小盲注，1000-2000元一个买进（绝对违法）。与人工智能1对1打head up，每小时要输220元，平均一天要输掉2200元，20天要输掉4.4万元人民币。
如果玩大的50/100元盲注，2万元一个买进，如1元等于比赛里的1分($)，平均每天要输2.2万，20天要输掉44万元人民币。
而且，那4位选手是世界排名前15的1对1的扑克玩家，对于多数休闲娱乐的德州扑克玩家，输牌的速率可要翻倍的，也就说打5/10元盲注，每小时会输上440元，打50/100元盲注，每小时会输上4400元，20天要输掉88万元人民币。
如果有人会问，如果把这个人工智能程序拿来，然后连接到国外扑克网站Poker star，Full Tile上赢美刀多爽啊。德州扑克有10^160可能性，运行该程序所需的超级电脑。价格可能数百万美金不止，估计每小时消耗耗的电费都要比赢来的钱还多。




德州扑克是赌博，还是技巧？
德州扑克有运气成分，但比赛总共进行12万手牌，牌运的影响几乎微乎其微。打100-1000手牌，运气还是影响很大的；但打了12万手牌赢到17.66万个盲注，比赛结果的可信度高达99.77%。
也就是说，每场比赛打12万手牌，人类与AI进行1000场比赛，AI将赢下998场，人类只能赢下2场。因此，人工智能Libratus 有着完全不可逆转的优势。
也就是说，每场比赛打12万手牌，人类与AI进行1000场比赛，AI将赢下998场，人类只能赢下2场。因此，人工智能Libratus 有着完全不可逆转的优势。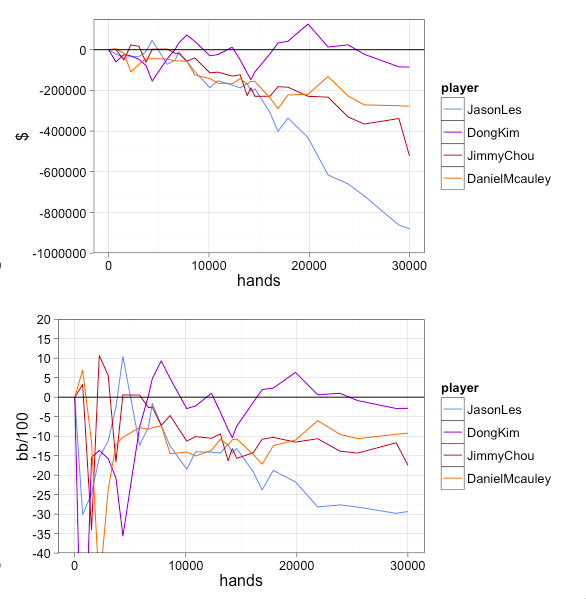



即使同为顶级高手的4位扑克玩家，在对局人工智能的成绩中，他们的实力也分出高下。
在与同样AI对局3万手牌后，四个玩家成绩分出档次，其中Dong Kim 输掉856个盲注，比Jason Les 输掉了8800个盲注的成绩好10倍。另外，两名玩家各自输了2776个盲注，5728个盲注。
如果这四个人相互对局3万手牌，Dong Kim 与 Jason Les对局，那他也会赢到8800-856 = 7944个盲注，也许会有上下1000个盲注的波动。总之Dong Kim 的牌技优势还是高于Jason Les ，但要打上万手牌才能分出胜负。

4位选手的实力：
一直说这4位选手为世界顶级扑克玩家，可大多数扑克迷都没听说过他们。怎么没有 Phil Ivey, Daniel Negreanu，Tom dwan这些扑克明星呢？
其实，大家每天在视频上看到的那些扑克界的明星都是5-6年前的对局了。当网络扑克兴起后，大量优秀的扑克玩家涌现。任何事情搬到到互联网上，发展速度都变得惊人。5年的扑克水平在网络上能赢到100万美金，5年后却只能输钱，所以原来的高手，并不是现在高手。如今让Daniel Negreanu 到 Poker Star 打1/2美元的游戏，他未必定能赢到钱。
另外，这场人类与AI的对局要每天打8-10个小时，打上20天，奖金还不到20万美金。Tom dwan在澳门赌场里一手牌输掉1100万美金。所以他们不屑于为了这么点奖金，打这么漫长的比赛。
在2005年以前，互联网扑没兴起时候，人们普遍在线下打扑克，一小时打上20手牌，要练成一个优秀的扑克选手至少要2-3年，而且还要有高手指点。大多数人打了7-8年扑克还是同样的臭水平，那时候高深的扑克知识也并不普及，多数扑克书籍都是垃圾。
而2005年后有了互联网扑克，人们1个小时能打1000收牌，速率提高50倍，职业玩家1年能打上千万手牌。各种高深的扑克技巧在网上到处都能找到，于是互联网扑克水平变得越来越高，而且每年都在不断发展新的扑克技巧。
以上那4位高手，在网络进行上千万手牌的对局，都是各大扑克网站1对1赢牌率最高，他们征服了忽略网就必然征服整个扑克界。
而且，2人德州扑克是技巧性最强的对局模式。在多人对局德州扑克游戏，拿到强牌的概率高，没有牌的时候就可以扣掉，损失很少。而2人对局扑克，每次扣牌就丢掉1.5盲注，跟注时拿到强牌的机会很少。因此，2人德州扑克对局更多的bluff，发现并打击对手的弱点，依靠策略才能赢牌。
当人工智能以巨大的优势战胜这4位高手，可以肯定世界上没人能打败人工智能Libratus。因为Libratus是根据纳茨博弈理论，经过Counterfactual Regret Minimization（反事实思维） 方法学习后，形成最完美的扑克打法。

人工智能在扑克的应用：Counterfactual Regret Minimization
反事实思维是个体对不真实的条件或可能性进行替换的一种思维过程。反事实思维（counterfactualthinking）是美国著名心理学家、诺贝尔经济学奖获得者Kahneman提出的。
例如：生活中有一种心理现象，就是思维活动针对的不是已发生的事实，而是与事实相反的另一种可能性。人们迟到的时候，会寻思“如果早点动身就不会迟到了”；人们考砸的时候，会寻思“要是再加把劲这次考试就能及格了”。所谓反事实思维，就是与事实相反的假想。
反事实思维是对过去已经发生过的事件，之后进行判断和决策后的一种心理模拟（mentalsimulation）。反事实思维通常是在头脑中对已经发生了的事件进行否定，然后表征原本可能发生但现实并未发生的心理活动。它在头脑中一般是以反事实条件句的形式出现。反事实条件句（counterfactualconditionals）也叫“虚拟蕴涵命题”，它具有“如果……，那么……”的形式。
例如：“如果刚才没买那件衣服，现在就可以买这件了。”一个反事实思维包括两个部分：虚假的前提（“如果刚才没买那件衣服”）和虚假的结论（“现在就可以买这件了”）。
其实，这也是人类学习扑克的一种模式，即试错模式。每次输了一手大牌后，最好想如果我当时不去加注，不去跟注，或者扣牌，就不会输了。每次对过去的行为感到后悔，然后总结经验，调整打法，看是否赢得更多的钱。或少输钱。
当然，这是一种非常慢的自学方式，人类更多是从互联网学习别人已经总结好的正确打法。然后，在加以练习，比如每天打上4-5个小时，再花1-2个小时总结今天打扑克的错误和进步，一般6个月里在互联网上打300—500万手牌，通常能成为优秀的扑克玩家。
扑克人工智能是通过Counterfactual Regret Minimization进行100万亿手牌的训练来形成一套完美的打法。
当然这还远远不够，扑克的完美打法是根据不同的对手，在不同时间段，进行调整的。比如对抗攻击性极强的玩家，与打牌很紧的玩家的打法是不同的。
例如： 一个打法疯狂的玩家100个大盲注全压，拿AJ，AQ，TT，99 以上的牌跟注就足够了，但如果一个打牌非常紧的玩家100个盲注全压，至少要AK，QQ以上的牌才能跟注。
因此，人工智能还必须根据近期相关性的牌局，来调整自己的打牌的范围，进而适应不同对手，不同的打法。这就需要另一项技术应用recursive reasoning 来进行 Continuous Re-Solving。。。
这使得系统逐渐补救了战术中的漏洞，最终如桑德霍姆描述为“系统大举获胜，结果很显著”。
　　“比赛到一半的时候，我们真的以为要赢了，”其中一位专业玩家丹尼尔. 麦考利(Daniel McAulay)说。“我们真的有机会打败它。”
　　卡内基梅隆大学团队每晚用超级电脑来分析白天的比赛，提高系统性能。系统检测自身在每轮比赛中的弱点，每天补救三个最明显的失误，而不是试图学习对手的制胜战术。
　　这个方法最终使其出其不意用大赌注智胜它的对手，桑德霍姆称之为系统相对人类“心理承受能力”的优势。
　　相对其它玩扑克的程序，Libratus最主要的提高在于电脑在接近游戏最后时的玩法。先前的系统从头至尾使用单一战术，但是Libratus使用额外的反馈回路来实时回应对桌的人类。
　　“我们用了所有能想到的办法，它实在是太强大了，”另一位扑克玩家杰森.莱斯(Jason Les)说。“它每天的出现都让我们士气低落，最后输的这么惨。我以为我们最后的筹码会非常接近。”
　　桑德霍姆说，几乎可以肯定要单独成立一家新的创业公司，用Libratus背后的技术来开发商业用途。他已经研究了27年的谈判策略。他早先开发过的一款程序被2/3的美国器官移植中心使用来决定哪位病人可以得到新肾的移植。
太累啦！o (╯□╰)o
后面文章以后在翻译啦，如果这篇文章上知乎日报的话，可以考虑 ( ´◔ ‸◔`)

如果大家对人工智能感觉太抽象，很难理解，可以看本人写过的一篇人工智能的应用介绍，简单易懂，初中生就能明白。Introduction to CMAC Neural Network with Examples
http://skyocean117.blogspot.co.nz/2013/12/introduction-to-cmac-neural-network.html

下面是扑克人工智能Libratus的设计理论，项目主任的讲座视频，大家翻墙自己看去吧!
https://www.youtube.com/watch?v=QgCxCeoW5JI




However, how the opponent’s actions reveal that information depends upon their knowledge of our private information and how our actions reveal it. This kind of recursive reasoning is why one cannot easily reason about game situations in isolation,
which is at the heart of local search methods for perfect information games. Competitive AI approaches in imperfect information games typically reason about the entire game and produce a complete strategy prior to play (14, 15).2 Counterfactual regret minimization (CFR) (11, 14, 17) is one such technique that uses self-play to do recursive reasoning through adapting its strategy against itself over successive iterations. If the game is too large to be solved directly, the common solution is to solve a smaller, abstracted game. To play the original game, one translates situations and actions from the original game in to the abstract game.
While this approach makes it feasible for programs to reason in a game like HUNL, it does so by squeezing HUNL’s 10160 situations into the order of 1014 abstract situations.

DeepStack takes a fundamentally different approach. It continues to use the recursive reasoning of CFR to handle information asymmetry. However, it does not compute and store a complete strategy prior to play and so has no need for explicit abstraction. Instead it considers each particular situation as it arises during play, but not in isolation. It avoids reasoning about the entire remainder of the game by substituting the computation beyond a certain depth with a fast approximate estimate. This estimate can be thought of as DeepStack’s intuition: a gut feeling of the value of holding any possible private cards in any possible poker situation. Finally, DeepStack’s intuition, much like human intuition, needs to be trained. We train it with deep learning using examples generated from random poker situations. We show that DeepStack is theoretically sound, produces substantially less exploitable strategies than abstraction-based techniques, and is the first program to beat professional poker players at HUNL with a remarkable average win rate of over 450 mbb/g.
Continuous Re-Solving
Suppose we have a solution for the entire game, but then in some public state we forget this
strategy. Can we reconstruct a solution for the subtree without having to solve the entire game
again? We can, through the process of re-solving (17). We need to know both our range at
the public state and a vector of expected values achieved by the opponent under the previous
solution for each opponent hand. With these values, we can reconstruct a strategy for only the
remainder of the game, which does not increase our overall exploitability. Each value in the opponent’s
vector is a counterfactual value, a conditional “what-if” value that gives the expected
value if the opponent reaches the public state with a particular hand. The CFR algorithm also
uses counterfactual values, and if we use CFR as our solver, it is easy to compute the vector of
opponent counterfactual values at any public state.
Re-solving, though, begins with a solution strategy, whereas our goal is to avoid ever maintaining
a strategy for the entire game. We get around this by doing continuous re-solving:
reconstructing a strategy by re-solving every time we need to act; never using the strategy beyond
our next action. To be able to re-solve at any public state, we need only keep track of
our own range and a suitable vector of opponent counterfactual values. These values must be
an upper bound on the value the opponent can achieve with each hand in the current public
state, while being no larger than the value the opponent could achieve had they deviated from
reaching the public state.5
At the start of the game, our range is uniform and the opponent counterfactual values are
initialized to the value of holding each private hand at the start.6 When it is our turn to act

纳茨均衡：
Exploitability The main goal of DeepStack is to approximate Nash equilibrium play, i.e., minimize exploitability. While the exact exploitability of a HUNL poker strategy is intractable to compute, the recent local best-response technique (LBR) can provide a lower bound on a strategy’s exploitability (20) given full access to its action probabilities. LBR uses the action probabilities to compute the strategy’s range at any public state. Using this range it chooses its response action from a fixed set using the assumption that no more bets will be placed for the remainder of the game.

我的麻将机在升降起来之后，我没注意结果少放进去一张牌，然后麻将机就不能再玩了，它洗牌好久，也不能再升降了。打开面板里面一副麻将已经摆好了，但不能升降，洗牌的地方是空的，是要把另一副麻将倒进去么？